머신러닝 핵심 개념 이해 (3) | Linear Regression

안녕하세요?

오늘은 구름 인공지능 교육에서 배운 머신러닝 핵심 개념 이해를 복습해보는 3번째 시간입니다. 

오늘은 Linear Regression을 중점적으로 복습하고자 합니다.

---

Linear Regression (선형회귀) 란?

• 종속 변수 y와 한 개 이상의 독립 변수 (또는 설명 변수) x 사이의 선형 상관 관계를 모델링하는 회귀분석 기법
• 즉, 정답이 있는 데이터의 추세를 잘 설명하는 선형 함수를 찾아 x에 대한 y를 예측
• 선형회귀의 일반적인 형태 :  Linear Combination 

• 1개의 독립변수(x)가 1개의 종속변수(y)에 영향을 미칠 때 : 단순 회귀분석 (simple regression anlysis)
• 2개 이상의 독립변수가 1개의 종속변수에 영향을 미칠 때 : 다중 회귀분석 (multivariate regression anlysis)
• 예시) 단순 회귀분석 vs 다중 회귀분석

• => 가장 적합한 θ들의 set을 찾는 것이 목표 !!!
  • 그렇다면 우리가 찾은 θ가 적합한지 어떻게 알까? ( = 좋은 선형회귀 모델인지 어떻게 알까?)
  • -> 이럴 때 사용하는 것이 cost function

 

Cost Function (비용함수) 에 대하여

• 예측 값과 실제 값의 차이를 기반으로 모델의 성능 (정확도)을 판단하기 위한 함수
• Linear Regression의 경우 Mean Squared Error Function (평균 제곱 오차 함수)를 주로 사용

• => MSE(Cost, J(θ))가 최소가 되도록 하는 θ를 찾아야 한다.!!
  
  • 어떻게 찾을까?? -> Gradient Descent Algorithm
• + MSE외의 비용함수 : MAE(absolut), MAPE(percentage), RMSE(root)
  • MSE와 MAE는 장단점이 다름 : MAE가 MSE보다 이상치에 대한 error가 적게나옴 (MSE는 제곱을 해서 이상치를 민감하게 받아들임)

 

Gradient Descent Algorithm (경사하강법)에 대하여

• Cost Function의 값을 최소로 만드는 θ를 찾아나가는 방법
• Cost Function의 Gradient에 상수를 곱한 값을 빼서 θ를 조정
• 즉, Cost Function에서 경사가 아래로 되어있는 방향으로 내려가서 Cost가 최소가 되는 지점을 찾는다.
• 어느 방향으로 θ를 움직이면 Cost값이 작아지는지 현재 θ 위치에서 Cost 함수를 미분하여 판단 (Gradient = 기울기!!)

• Gradeint Descent Algorithm 방법
  1. 변수(θ)의 초기값을 설정
  2. 현재 변수 값에 대응 되는 Cost Function의 경사도 계산 (미분)
  3. 변수를 경사 방향(기울기의 음의 방향 = Gradient의 음의 방향)으로 움직여 다음 변수 값 설정
  4. 1~3을 반복하며 Cost Function이 최소가 되도록 하는 변수 값으로 근접해 나감 (= 전체 Cost 값이 변하지 않거나 매우 느리게 변할 때까지 접근)
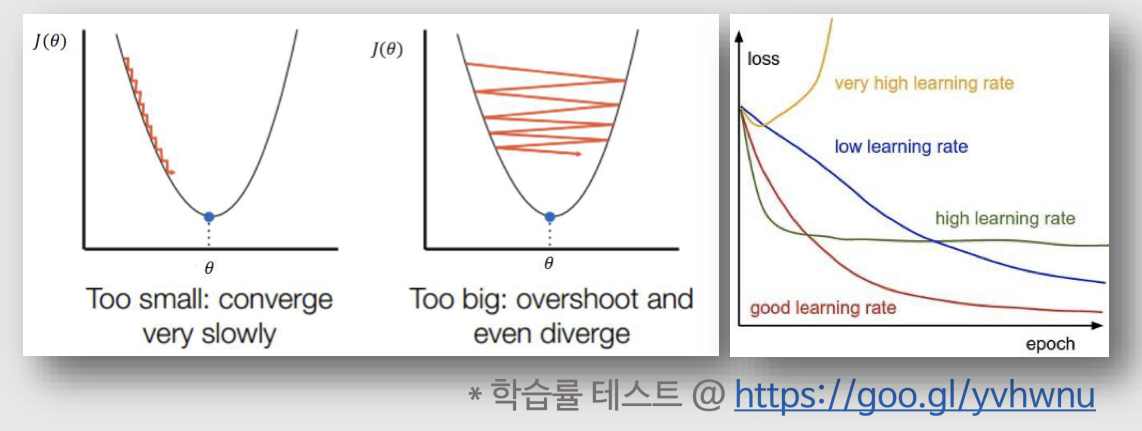
• 식에서 α 는 사람이 결정해주는 Hyper-Parameter로 Learning Rate (학습률)을 나타냄 : 얼마나 큰 보폭으로 움직일지를 결정

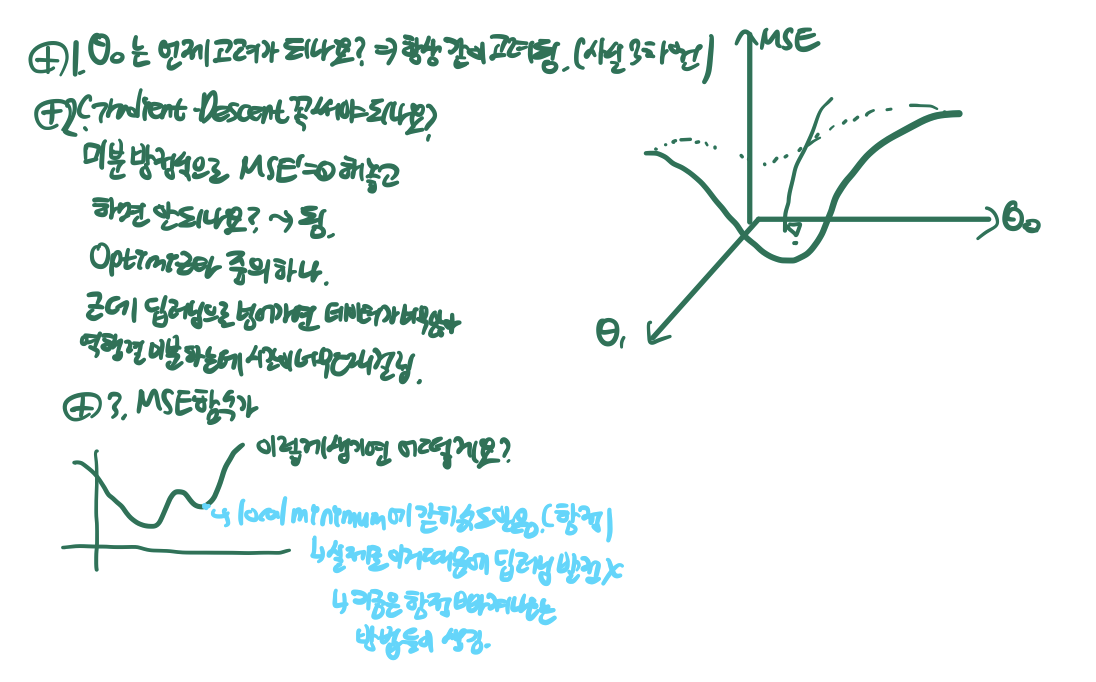
• 나올 수 있는 질문들
  
  1. θ0 는 언제 고려가 되나? -> 항상 같이 고려됨 (사실 cost func 모양은 3차원 그 이상)
  2. gradient descent 말고 그냥 미분방정식으로 (MSE)'=0 해놓고 해결하면 안되나? -> 가능함. 미분방정식 풀이도 optimizer중의 하나임. 그러나 딥러닝으로 넘어가면 데이터값이 너무 많아 역행렬 미분을 하는데 시간이 너무나도 오래 걸림
  3. MSE 함수가 구불구불하게 (여러번 꺾이듯이) 생기면 어떻게 하나? -> local minimum에 갇힐 수도 있음 (함정임), 실제로 이 문제를 해결하지 못해 딥러닝의 발전이 더뎠던 순간도 있었음 (지금은 이 함정을 빠져나가는 여러가지 방법들이 생김)