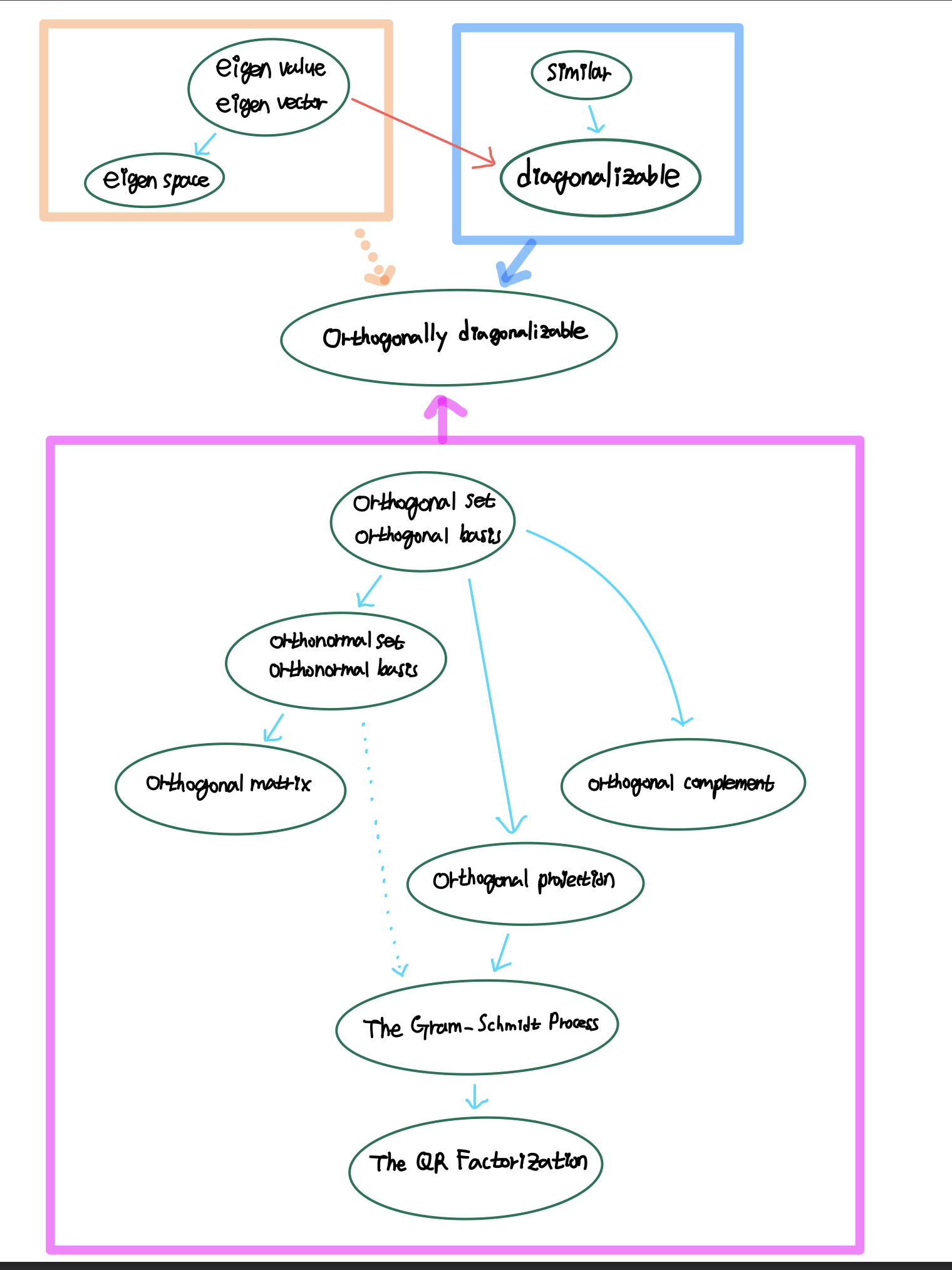
eigen, diagonal, orthogonal

안녕하세요?
개강이 얼마남지 않았네요..ㅎㅎ
요즘 학부인턴을 시작하고 인공지능 스터디 모임과 함께 개강준비를 하고있다보니 선형대수 공부에 점점 소홀해 지고 있는 것 같습니다..

일단 이제 개강하면 뭐 대학에서 배울거니까..라는 생각도 들고..ㅠㅠ

그래도 오늘은 공부 끄적끄적이라도 한 흔적을 좀 가지고 왔습니당

고윳값, 대각화, 직교 부분을 공부하다보니 또 이부분들은 세부분이 서로 열결되어있는 부분들이 많이 있는 것 같아서..
어떻게 순서대로 연결되는지 궁금해서 그냥 무작정 개념이랑 중요 이론들 쭈우우욱 써보았씁니다.ㅋㅋㅋㅋㅋ ㅎ

예제푸는거랑 이론 증명하는 것도 중요한데 그건 뭐 책에 많으니깐..
그런 것도 중요하지만 개념들이 서로 어떻게 연결되어있나 긴밀히 파악하는 것도 중요하다고 생각합니다.
(뭐 그래도 개념을 완벽히 제자신에게 받아들여지려면 예제 푸면서 이해하는 것도 엄청 중요하다고 생각해요.!)

그런데 요즘 이부분 공부하면서 느낀건데..
선형대수라는 과목이 정말 분야가 넓은 것 같습니다.ㅋㅋㅋ
유클리디안 공간, 벡터공간, 내적공간, 직교공간, 복소공간 등등등등등 또 그속에 등장하는 수많은 개념들과 정리들..
정말 배우면 배울수록 얼마나 방대한 내용들을 배우고 가는지 실감이 납니다..ㅎ

오늘은 eigen -> diagonal -> orthogonal 개념들이 서로 어떻게 연결되어있는지 보고 싶어서 가져왔는데
사실 이 세 개념들이 마지막에 최종적으로 만나는 곳은 SVD입니다.
그런데 SVD부분은 뭐랄까.. 아직 이해를 거의 못한느낌..이라서..ㅋㅋㅋ
그부분은 담에 기회가 되면 공부하고 그건 세세히 정리해서 포스팅 해보도록 하겠습니다.!